The Long and Short: Can Hedging Negative Convexity Impact the Level of Interest Rates?

Negative convexity is a feature often found in callable bonds and mortgage backed securities. For this blog, the focus will be on agency MBS. Its source is the embedded option that allows for prepayment of principal prior to final maturity. This blog will examine negative convexity, how portfolio managers can hedge the risk associated with negative convexity, and how interest rate swap and swaption dealers manage the risk that has been transferred to them by the portfolio managers. (For this blog, we take a very broad view of the definition of portfolio managers which may include insurance companies, pensions funds, mutual funds and of course Fannie Mae and Freddie Mac.)

Why write this blog now? Over the past year, interest rates have been trending down. In addition, over the past 1½ months, rates have dropped and then backed up. Figure 1 shows the 10-year Treasury Constant Maturity Rate from mid-September 2018 to September 9, 2019. Rates were above 3.20% and as low as 1.47% during that time period. That is a pretty big move in one year. Figure 2 also shows the 10-year Treasury Constant Maturity Rate, but for a shorter time period – from mid-July 2019 to September 9, 2019. This shows a drop from 2.13% to 1.47% and back up to 1.90% in less than two months. These changes in interest rates can lead to significant hedging activity as explained below.

Figure 1

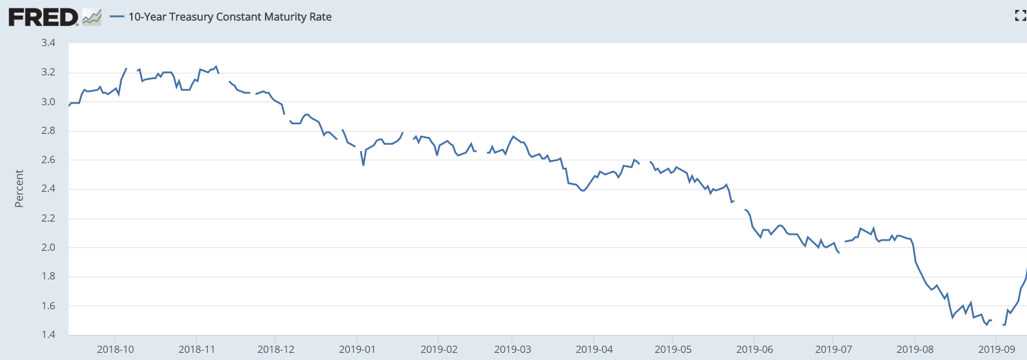
Figure 2

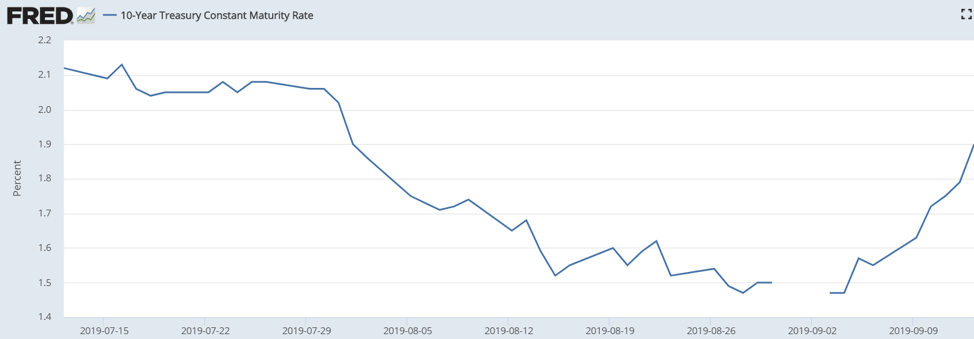
Source for both graphs: https://www.stlouisfed.org/– Please note the gaps in the graphs are from the source document

What is Negative Convexity

To help understand negative convexity, let’s first look at an example of positive convexity. Assume a bond has a coupon of 4%, semi-annual payments, and a maturity of 10 years. Looking at Table 1, we can see our bond has a price of a 100, or par, when the yield is 4%. Now assume the yield changes by 100 basis points to 3% or 5%. In each case, we can see the corresponding price and percentage price change.

Using 4% as our base case scenario, the yield changes on a linear basis by 100 basis points whether we move to 3% or 5%. Notice, however, that the percentage price change is greater with a downward move in yield. This feature, where the percentage price change is greater for a downward move in interest rates than for the same corresponding upward move in interest rates, is known as positive convexity.

Now assume that the bond has an embedded option allowing the borrower to prepay principal at their option. This is known as prepayment risk – from the owner of the security’s perspective. For ease of illustration, assume the borrower will prepay a portion of the principal at par when rates fall below 4%. Table 2 illustrates the new prices for the 3 potential scenarios:

Comparing the results in Table 2 with those from Table 1, it is evident that the prepayment option negatively affects the investor’s return when interest rates fall from 4% to 3%. There are two ways to view negative convexity. A practical analysis is when interest rates fall, the price of MBS and other securities with embedded options will rise less than other securities that do not have a prepayment option. The technical definition can be seen in Table 2 when we compare the percentage price change for a 100 basis move down in rates, a positive 2.50%, to the percentage price change, a negative 7.79%, for the same corresponding upward move in interest rates. Clearly the price appreciation is less than the price depreciation for the linear basis point movement. In this example it is 100 basis points.

The Impact on Average Life and Interest Rate Risk

Now let’s add in the impact on the average life of the security. Assume the average life of the security is as follows:

The results in Table 3 demonstrate that when yields drop, the mortgage backed security’s average life will fall, or contract, to 3.2 years. The opposite occurs when interest rates move up, the average life extends out. These are known as contraction and extension risk, respectively, and both result from the prepayment option.

These risks, contraction and extension, are what portfolio managers attempt to hedge. Why? It is important to understand that the features of contraction and extension apply not only to single instruments but to portfolios as well. If a portfolio has significant holdings in mortgage backed securities, any change in interest rates will impact the average life and consequently, will impact the effective duration of the portfolio.

One of the most important aspects of managing a portfolio is to manage and mitigate interest rate risk. When interest rates go down, the duration of the portfolio will decrease. Conversely, when interest rates go up, the duration of the portfolio will increase. Portfolio managers will manage duration around specified risk limits established by the company’s board and senior management. For instance, Fannie Mae and Freddie Mac traditionally have managed their duration to “0”. Clearly, any change in average life will lead to an adjustment in their portfolio to bring the effective duration back to zero.

Hedging Negative Convexity

To manage contraction risk, the portfolio manager can hedge by either:

1. receiving fixed in the interest rate swap market,
2. buying Treasuries (Treasury futures may also be used), or
3. purchasing a payers swaptions.

Let’s assume that a portfolio manager decides to execute all of these strategies. Let’s also assume that the potential move, or the current interest rate volatility, is more pronounced than business as usual. This will increase the amount of hedging activity. The amount of hedging activity would have to be substantial to impact the level of interest rates.

Let’s look at the strategies first from the portfolio manager’s perspective and then from the swap dealer’s perspective. From the portfolio manager’s perspective:

1. The purchase of U.S. Treasuries will put upward pressure on prices and downward pressure on yields. This will occur at the intermediate and long-end of the curve which may potentially steepen the curve.
2. The following shows the portfolio manager receiving fixed. This will lead to spreads narrowing

 

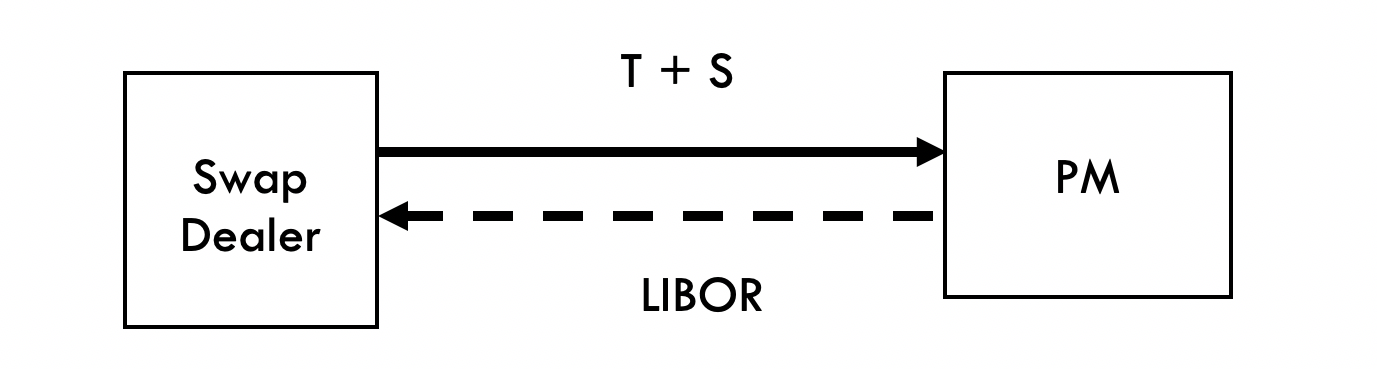
3. In the swaption market, the portfolio manager pays a premium for the right to receive fixed. This will increase the volatility in the swaptions market.

Now let’s examine this from the swap and swaption dealer’s position:

1. When the interest rate swap dealer pays fixed, they will buy Treasuries to hedge. This puts upward pressure on prices and downward pressure on yields. This corresponds to bullet point number two above.
2. To hedge in the swaptions market, the dealer will delta hedge by purchasing Treasuries. This will also have the impact of driving prices higher and yields lower. As an aside, the swaption dealer will continue to markup volatility assuming there is continued purchasing of swaptions.

The opposite strategies would be employed for extension risk. This would have the opposite impact on interest rates. Specifically, putting upward pressure on interest rates. Again, it needs to be emphasized that the above scenarios will occur with significant hedging activity whether for managing contraction or extension risk.

In conclusion, hedging negative convexity is in effect managing interest rate risk. A variety of interest rate risk mitigating strategies can be employed. These strategies can lead to significant one-way trading thereby influencing the direction of interest rates.

To learn more about hedging strategies and managing interest rate risk, contact GFMI about bringing one of our Capital Markets or Derivatives courses to your organization.