As Safe as Houses? Central Counterparties and Risk

In Britain, if you say that someone or something is ‘as safe as houses’, you mean that it is completely safe. But is this the case with Central Counterparties, which were designed to provide a level of security in taking on the risk between parties in financial transactions?

In September 2018, a single Norwegian power trader who was clearing his own trades suffered massive losses on positions in the spread between the Nordic and German power markets. The trader could not meet margin calls and was declared in default by Nasdaq Clearing, who were acting as central counterparty to the trades. The positions were closed out through an auction to other clearing members, but losses on the portfolio exceed the defaulting member’s margin collateral and default fund contribution by €114 million (over US $129 million. These losses were met by Nasdaq Clearing’s own (junior) capital contribution to the default waterfall (€7 million) and by default fund contributions of non-defaulting members (€107 million).¹

The losses suffered on this trade were not large relative to the size of the global derivative market,²and order was quickly restored. Nasdaq Clearing replenished its junior capital contribution immediately following the default, and the default fund was restored within one week through additional assessments on clearing members.³But, in the well-ordered world of central clearing, defaults that result in losses to non-defaulting clearing members are rare,⁴and the excess losses to be absorbed in this incident were reported to be over two-thirds of the total default fund.⁵

In the new regulatory framework for derivatives constructed since the financial crisis, clearing by central counterparties (CCPs) plays a critical and much-expanded role. World leaders agreed at the G20 summit in Pittsburgh in 2009 that all standardized derivatives should be centrally cleared, and the Basel III reforms have included incentives to choose central clearing over bilateral counterparty risk management. In making this choice, regulators were motivated by a desire to reduce bilateral concentrations of counterparty risk, increase transparency, and limit the risk that financial stress might be transmitted through the financial system by contagion. They were also influenced by the long history of CCP resilience in the face of financial stress. But increased reliance on central clearing creates complex interconnections between CCPs, their clearing members, and other market participants. These interconnections may themselves be a source of systemic risk, either directly through failure of a CCP, or indirectly due to liquidity and contagion effects related to failure of a clearing member or a large client.

Regulators have responded to these concerns by developing stricter standards for CCP risk management, expressed in the Principles for financial market infrastructures(PFMI) published jointly by the Committee for Payments and Market Infrastructures (CPMI) of the Bank for International Settlements and the Board of the International Organization of Securities Commissions (IOSCO) in 2012,⁶for which CPMI-IOSCO published further guidance on CCP resilience in 2017.⁷Implementation of and adherence to these standards has made CCPs better able to withstand participant failure and other stress events, but risk management in centrally cleared markets remains challenging.

In particular, CCPs use complex models to determine margin requirements, as well as stress tests to determine the financial resources that the CCP and its clearing members must commit in order to absorb losses not covered by margin collateral. If these models or the risk management structure in which they are embedded fail, CCPs may be unable to contain and control counterparty risk in the way that regulators expect. As the Nasdaq Clearing case showed, even a default that is contained by the default waterfall may impose significant financial and liquidity costs on non-defaulting members: central clearing is not without risk. A default or series of defaults large enough to result in the failure of a CCP would significantly disrupt the global financial system, particularly since there are few substitutes for most systemically important CCPs.⁸

So, should we be worried? Are CCPs ‘as safe as houses’, or do events like the Nasdaq Clearing member default reveal cracks in the armor that central clearing is meant to provide against systemic risk linked to counterparty failure? In the remainder of this article, we look more closely at what CCPs are, what they do, and how they use models to manage risk. By doing so, we hope to cast light on these critical questions.

What is a CCP?

A CCP is best understood as a commitment mechanism. Its primary function is to ensure that clearing members meet their obligations in accordance with the CCP’s rules. It does this by becoming a counterparty to every trade through a process called novation. In novation, the original contract between the buyer and seller in a transaction is replaced by two new contracts, one between the CCP and the buyer and another between the CCP and the seller. The CCP thus becomes the buyer to every seller and the seller to every buyer.

By substituting itself for the original buyer and seller, the CCP permits multilateral netting of positions. Thus, for example, offsetting transactions in the same contract that a party enters into with two different counterparties will be genuinely extinguished once they are novated to the CCP, rather than just having offsetting market risk. Similarly, positions in related contracts (e.g., futures and options on the same underlying source of risk) that were originally transacted with different counterparties may benefit from correlation-related offsets once they become part of a combined portfolio of positions with the CCP.

Novation to a CCP also helps solve the problem of commitment in financial markets. If both parties could commit to meeting their future contractual obligations, then there would be no need for clearing by a third party. In practice, however, either party to a contract may fail to meet its future obligations; in derivatives markets, this is known as counterparty risk or counterparty credit risk. By acting as a substitute counterparty, the CCP helps ensure that each side meets its obligations over the life of the trade.⁹If a clearing member defaults, then the CCP takes responsibility for settling the defaulting member’s trades. In doing so, of course, it may suffer a loss. In order to ensure that it is able to meet its obligations, the CCP takes collateral (in the form of margin) from both counterparties to the original transaction. The CCP also requires all clearing members to contribute additional resources to a default fund, through which losses will be mutualized if they exceed the margin collateral and default fund contribution of the defaulting member. This, as we have seen, is what happened in the Nasdaq Clearing member default.

A CCP can also be understood by thinking about what it is not. For example, a CCP is not a bank. Banks are risk takers who intermediate between short-term funding (e.g., deposits) and long-term lending (e.g., mortgage loans). Bank balance sheets are characterized by significant mismatch between assets and liabilities, and taking exposure to credit, interest rate, liquidity and other risks is the core of a bank’s business. CCPs, by contrast, are risk managers who serve as substitute counterparties on both sides of a transaction brought to them by clearing members. Since they are the buyer to every seller and the seller to every buyer, they have a matched book in which every long position is offset by an equal and opposite short position.¹⁰

This matched position means that CCPs face very little market risk. They do, however, face significant counterparty risk. Should a clearing member default, the CCP will use margin collateral and other prefunded financial resources to meets its obligation to settle the transactions; this may include capital contributed by the CCP itself. It must also enter into replacement trades to restore its matched book. Since it may only be able to do so at a loss, it is exposed to counterparty risk related to this replacement cost. In addition, default by a clearing member will expose a CCP to liquidity risk, due to possible gaps between its immediate payment obligations and available financial resources.¹¹

A CCP is also not an insurer. The bilateral relationship between members who submit a trade for clearing is irrevocably terminated by novation. The original counterparties remain connected only through contingent exposure to mutualized loss absorption in the default fund. Excess losses are mutualized in a CCP, but clearing members derive only limited benefits from risk pooling and diversification across members, which are central drivers of the services provided by insurers.¹²

How Do CCPs Manage Risk?

CCPs use a sequence of prefunded financial resources to manage losses caused by a participant default. These prefunded financial resources constitute the default waterfall.

Margin is one part of the waterfall. It ensures that participants only take on positions that they are prepared to collateralize. In addition, participants must contribute to a default fund, which is used to cover losses that exceed margin requirements. The CCP also contributes some of its own funds to the waterfall.

In the event of participant default, these funds are applied in a particular order. The margin provided by each clearing member is the first level of defense against losses due to default by that member. The defaulting member’s own contribution is the second line of defense. The CCP provides a third line of defense through its own funds, which is sometimes called the CCP’s ‘dedicated amount’ or ‘junior capital’. Any losses that cannot be absorbed by these first three lines of defense are then allocated to non-defaulting members on a mutualized basis, through their contributions to the default fund. An illustrative example of the default waterfall of a particular CCP, Eurex Clearing, is shown below:¹³

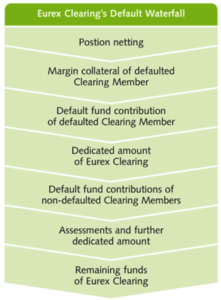
This waterfall, like that of other CCPs, embodies the principle of defaulter-pay loss allocation, in which the margin and other resources provided by the defaulting counterparty are used to protect the non-defaulting counterparties from loss. This is a key element of the incentive structure created by a CCP. Since each party knows that, should it default, its own financial resources will be used first, all parties are motivated to monitor and manage the risk in their positions.¹⁴In the absence of this incentive, the CCP would be exposed to considerable moral hazard, since participants might be tempted to pay less attention to risk and simply rely on the resources provided by the CCP and by other members to protect them from loss.¹⁵

Banks, by contrast, depend primarily on their own capital as protection against unexpected loss. We can think of this as survivor-pay loss allocation, in which the surviving (i.e., non-defaulting) entity, the bank, uses its own financial resources to absorb losses arising from the default of others (e.g., obligors who default on loans from the bank).¹⁶CCPs do contribute some of their own funds to the waterfall, but CCP capital cannot be the primary financial resource for absorbing default losses without undermining the defaulter-pays loss allocation principle on which the incentive structure depends. Capital thus plays a very different role in managing risk in CCPs than it does in banks.¹⁷

The junior capital or dedicated amount contributed by the CCP is important, however, in demonstrating the CCP’s commitment to managing risk, since it provides the CCP with ‘skin in the game’. Its location within the waterfall is also critical. By applying its own funds ahead of those of non-defaulting members, the CCP expresses faith in its own risk management mechanisms and provides participants with an additional layer of protection against losses arising from the default of others. Failing to do so could damage a CCP’s reputation.

Consider, for example, the case of KRX Clearing. In December 2013, a defective trading algorithm led to the sudden collapse of HanMag Securities, a clearing member of the Korea Exchange (KRX). The default waterfall rules did not require any junior capital contribution by KRX, which acts as its own CCP, so losses in excess of the margin and other prefunded resources contributed by HanMag Securities were applied directly to the default fund contributions of non-defaulting members.¹⁸At least some of these members appear to have been unaware of the waterfall rules, and the unexpected losses that they suffered adversely affected confidence in the market.¹⁹KRX has since revised its waterfall rules to conform to international standards by placing its own junior capital contribution ahead of default fund contributions from non-defaulting members.²⁰

As the first line of defense, margin is critical to containing the impact of participant default. The margin system of a CCP has two components: variation marginand initial margin.

Variation margin is backward looking. It resets the exposure to the CCP to zero on a daily basis by transferring funds from the margin accounts of participants whose portfolios have suffered losses to the margin accounts of participants whose positions have made profits. For this reason, variation margin is typically not regarded as pledged collateral securing an obligation, but rather as final settlement of outstanding exposure.²¹

Initial margin is forward looking. It collateralizes potential future exposure due to market movements and other factors. This risk must be assessed over the interval between the last margin collection and the close out of positions following a participant default. This closeout period is called the Margin Period of Risk (MPOR). Margin calculations are based on possible price movements and liquidation costs over the MPOR.

Margin is calculated on a portfolio basis. This improves capital efficiency by taking into account possible offsets due to correlation or other forms of dependence between related positions. Since participants typically hold complex, heterogeneous portfolios, calculating the correct margin for a given portfolio is a non-trivial problem. CCPs solve this problem by constructing and applying a margin model. A CCP may use a different margin model for each set of products that shares similar risk characteristics and likely holding period following default. We discuss the use of models in CCPs, including margin models, in the next section.

Models in CCPs

The PFMI requires that a CCP “cover its current and potential future exposure to each participant fully with a high degree of confidence using margin and other prefunded financial resources.”²²CCPs that have complex risk profiles or that are systemically important in multiple jurisdictions should maintain sufficient financial resources to cover “the default of the two main participants or their affiliates that would potentially cause the largest aggregate credit exposure for the CCP in extreme but plausible market conditions.”²³This is known as the ‘Cover 2’ standard. Other CCPs must at least meet a ‘Cover 1’ standard: (i.e., they must maintain sufficient financial resources to cover the default of the single participant or its affiliates that would potentially cause the largest aggregate credit exposure for the CCP). A CCP is also required to “maintain on an ongoing basis sufficient liquid resources in all relevant currencies to cover its payment obligations.”²⁴

In order to ensure that they have sufficient financial and liquidity resources to meet these standards, CCPs make extensive use of models. Two types of models are of particular interest to us here. The first are margin models, which are used to determine the initial margin that each participant must provide as collateral against its portfolio of positions with the CCP. As we have seen, this margin is the first line of defense in the default waterfall. The second are models used to construct stress tests in order to determine the appropriate size of the default fund and to ensure that the CCP has adequate liquidity resources.

CCPs use a wide variety of models to calculate required margin. Different CCPs may use different models and different critical parameter values for the same products, and a CCP that provides clearing services across a range of products may use different modeling approaches for different products. Among the choices a CCP must make in constructing a margin model are which risk factors to model, the model type or framework (e.g., scenario-based or historical simulation), the look-back period (i.e., the historical data period used to estimate model parameters), the MPOR, the confidence level, and what correlation offsets to apply to portfolio-based margin calculations. Each of these choices involves potential risks and tradeoffs, and no single model or model type is superior in every application.

For example, scenario-based models such as Standard Portfolio Analysis of Risk (SPAN), which were first developed by the Chicago Mercantile Exchange (CME)²⁵, are flexible, relatively easy to understand, and have been successfully applied in many other markets. But they may be less well suited to complex portfolios that are subject to multiple sources of risk.²⁶In such cases, other models and risk measures, such as Value at Risk (VaR) or Expected Shortfall (ES) based on historical simulation, may be more appropriate. Similarly, using a longer look-back period to estimate the model will capture greater variety in the behavior of underlying sources of risk, but may make the calculated margin less sensitive to current levels of market volatility. Applying volatility scaling to historical simulation is one possible solution to this problem.²⁷

Estimating and modeling correlations is a particularly important problem in portfolio margin models. A CCP may allow reductions in required initial margin when a portfolio contains positions with risks that are correlated, for example because the risk in a long position in one contract is partly offset by the risk in a short position in another contract with which it is positively correlated. The reduction in portfolio risk, however, depends critically on the correlation relationship being statistically significant and reliable.

Consider again the Nasdaq Clearing member default that we described earlier. The member who defaulted had taken large positions in the spread between Nordic power prices and German power prices. Normally, this spread is relatively stable: the two sources of risk are positively correlated. On the day of the default, however, forecasts of heavy rain pushed Nordic power prices (which are heavily dependent on hydroelectric power generation) down, while a spike in carbon prices pushed German power prices up, as illustrated below:²⁸

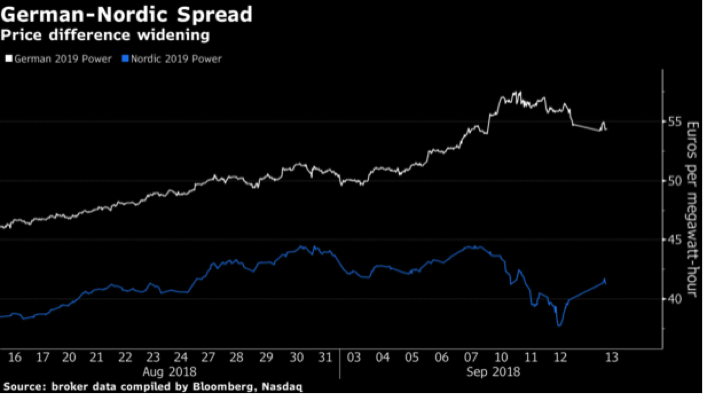
Nasdaq Clearing later reported that the spread change between the two markets on this day “was 17 times larger than the normal observed daily spread changes.”²⁹As we have seen, the losses on the portfolio exceeded not only the margin that Nasdaq Clearing had collected from the defaulting member, but also that member’s contribution to the default fund. This suggests that either the model used by Nasdaq Clearing to calculate the required margin on the portfolio or the stress tests used to determine the appropriate size for the default fund did not attach sufficient weight to the possibility that the correlation between the two power markets would break down in the way that it did on the day of the default.

In this sense, we can interpret the Nasdaq Clearing case as an example of model risk: the “risk of adverse financial … and reputational consequences arising from the design, development, implementation and/or use of a model.”³⁰Model risk is unavoidable in financial institutions, but it can be particularly problematic in CCPs, where models are central to constructing and calibrating the counterparty risk and default management mechanisms that are the CCP’s very reason for being. A critical element of risk management in a CCP, therefore, is daily back-tests to calculate required margin and to assess the statistical properties of the margin system.

Margin requirements are also sensitive to other characteristics of the portfolio or participant, such as illiquidity, concentration, credit risk, and possible wrong-way risk (i.e., adverse correlation between the value of the portfolio and the credit quality of the participant). Typically, these factors are addressed by calculating add-ons or multipliers to be applied to the margin requirement calculated by the margin model, rather than by incorporating them directly into the model. But these add-ons and multipliers are an additional source of model risk. For example, the defaulting portfolio in the Nasdaq Clearing case appears to have been particularly concentrated, and the trader himself subsequently suggested that the position was too large relative to the liquidity in the market.³¹The large losses suffered in the default suggest that the add-ons, multipliers or other risk controls applied to the portfolio may also have been inadequate to capture its true risk.

Since the financial crisis, stress testshave become increasingly central to risk management and supervision in financial markets. Banks use a wide variety of stress tests for internal planning and risk management purposes, and supervisory stress tests are used to assess bank liquidity and capital adequacy, as in the Comprehensive Capital Analysis and Review (CCAR) and Dodd-Frank Stress Test (DFAST) in the United States. As we have seen, however, a CCP’s own capital plays only a limited role in absorbing losses arising from counterparty default. Capital and balance sheet analysis of the kind usually applied to banks, including stress testing of capital adequacy, is therefore of limited value in assessing the safety and resilience of CCPs.³²Instead, CCPs carry out periodic stress tests to ensure that they have sufficient prefunded financial and liquidity resources to meet PFMI and regulatory coverage standards. Among other functions, these tests are used to determine the required size of the default fund and any junior capital contribution by the CCP to the default waterfall. They are meant to assess the likely performance of the CCP’s risk management structures across “a spectrum of forward-looking stress scenarios in a variety of extreme but plausible market conditions.”³³

For a CCP, these extreme but plausible market conditions must be conditioned on participant default. Default by a large participant may amplify stressed conditions the CCP faces in liquidating positions, and feedback from a first default may worsen the market conditions under which the CCP must liquidate positions if there is a second default. The scenarios used in CCP stress tests should therefore incorporate conditions for market liquidity and funding that are consistent with participant default. The impact of the adverse scenario must be evaluated under stressed conditions over the period required to liquidate the affected positions. This Stressed Period of Risk (SPOR) may be longer than the MPOR used to calculate required margin.

Typically, CCP stress tests use historical scenarios. This helps to incorporate peak historical volatilities, as required by the PFMI. But historical scenarios may not adequately capture a sufficiently wide range of extreme but plausible events, so it is usually necessary to supplement them with hypothetical and statistically generated scenarios. Constructing suitable scenarios and correctly modeling their impact on participant default and the CCP’s default waterfall and liquidity position is a further source of model risk. Sensitivity analysis (which assesses the impact of significant changes in margin system parameters and other elements of the risk management structure) and reverse stress tests (which attempt to identify plausible combinations of market stress and participant default that would result in failure of the CCP) are both critical to controlling this risk.

Beyond the Waterfall

To this point, we have concentrated on how CCPs use margin requirements, default fund contributions from clearing members, and their own junior capital to manage losses arising from participant default. Together, these constitute the prefunded financial resources available to the CCP. As the illustrative example for Eurex Clearing given earlier indicates, however, the default waterfall also contains other financial resources that may be used to contain losses and restore the CCP to health. The most important of these are assessments on clearing members (essentially, the right to demand that clearing members replenish their default fund contributions) and the remaining capital of the CCP.

The additional assessments that the CCP can ask of clearing members are capped, however, and the CCP’s own capital is finite. What happens if the resources available to the CCP are not sufficient to cover the losses arising from participant default? Should the CCP be allowed to fail, with possible systemic consequences? If not, who should bear the costs of CCP recovery (i.e., of restoring the CCP to viability), and how should this be achieved?

Given the lack of good substitutes for many systemically important CCPs, recovery mechanisms focus on continuity of service: their objective is to allow the CCP to continue to meet its obligations to participants over the relatively short time horizon in which those obligations fall due. Different CCPs may use different recovery mechanisms for the same products, and a CCP that provides clearing services across a range of products may use a different recovery mechanism for different products. The most common mechanisms are variation margin gains haircutting (VMGH),loss distribution charges, and contractual tear-ups.

Under VMGH, the CCP continues to collect variation margin payments that it is owed by clearing members, but conserves cash by canceling or reducing the variation margin payments that it would otherwise be required to make to clearing members. In this way, the CCP acquires cash to meet its short-term liquidity needs and may over time accumulate sufficient financial resources to be able to liquidate failed positions.³⁴

Loss distribution chargesare cash payments that the CCP demands from non-defaulting clearing members to meet default losses that exceed default resources, including assessments. Typically, each member must pay its pro rata share of the losses, based on its contribution to the default fund.³⁵

In a contractual tear-up, the CCP simply cancels some or all of its outstanding positions in contracts of a particular type. For example, a CCP that found itself, following a participant default, with long positions in a particular contract that were much larger than its outstanding short positions could elect to tear up sufficient long positions to restore its matched book.³⁶

Each of these recovery mechanisms has advantages and disadvantages. VMGH and contractual tear-ups make limited liquidity demands on clearing members, but they share losses unpredictably and unevenly among non-defaulting members. Loss distribution charges or other cash calls share the burden more equally, but the liquidity demands that they place on non-defaulting members may increase the risk of contagion during a period of stress.

In a highly severe loss scenario, of course, recovery may not be possible, and the CCP may fail. Like other financial institutions, CCPs are required to make plans for their orderly resolution in the event of failure. The failure of a systemically important CCP, however, would clearly have significant consequences for the orderly functioning of financial markets.³⁷

Conclusion

We have seen that a CCP is essentially a commitment mechanism that helps market participants control counterparty risk by acting as a substitute counterparty. It is a risk manager that runs a matched book, but it may be exposed to significant losses in the event of participant default. To manage these losses, the CCP constructs a default waterfall that incorporates a sophisticated margin system, a default fund composed of contributions from clearing members, and a limited amount of its own capital. The CCP’s rules allow it to impose assessments on non-defaulting members in order to replenish the default fund, and to make use of specific recovery mechanisms to restore its viability should the default waterfall be exhausted. The principles expressed in the PFMI and reflected in supervisory action by local regulators establish high standards for every element of this risk management framework that are intended to ensure CCP strength and resilience.

But we have also seen that the problem of risk management in CCPs is highly complex and model-dependent, with ample scope for misspecification, misestimation, and error. Losses will not always be limited to the margin and other prefunded resources contributed by the defaulting member, and the probability of failure of a systemically important CCP, while remote, is not zero. In a world in which regulatory and market pressures have concentrated large amounts of risk in CCPs and created complex interconnections between CCPs, their clearing members, and other market participants, such a failure would be highly disruptive.

In short, events like the Nasdaq Clearing member default do not reveal any fatal, hidden flaw in central clearing, or demonstrate the folly of increased reliance upon it. They do, however, serve as a timely reminder that CCP risk management, much like any house that is deemed to be ‘safe’, is imperfect. Models will sometimes fail and shifting a larger amount of the burden of counterparty risk management to CCPs has not magically caused that risk – or its possible systemic consequences – to disappear.

References

¹Nasdaq Clearing, https://business.nasdaq.com/updates-on-the-Nasdaq-Clearing-Member-Default/index.html(accessed 6 February 2019).

²The Bank for International Settlements estimates that the notional value of outstanding over-the-counter (OTC) derivatives was $595 trillion at end-June 2018, with gross market value of about $10 trillion. It estimates that the notional value of open interest in exchange-traded futures and options for the same date was about $93 trillion. See Bank for International Settlements, ‘Statistical release: OTC derivatives statistics at end-June 2018’, https://www.bis.org/publ/otc_hy1810.pdf(accessed 9 February 2019); and Bank for International Settlements, ‘Exchange-traded futures and options, by location of exchange’, https://www.bis.org/statistics/d1.pdf(accessed 9 February 2019).

³Nasdaq Clearing, https://business.nasdaq.com/updates-on-the-Nasdaq-Clearing-Member-Default/index.html(accessed 6 February 2019).

⁴J. McPartland and R. Lewis, ‘The Goldilocks problem: How to get incentives and default waterfalls “just right”’, Economic Perspectives (Federal Reserve Bank of Chicago), 1, 2017. On the history of CCPs in the United States, see R. Kroszner, ‘Can the Financial Markets Privately Regulate Risk?: The Development of Derivatives Clearinghouses and Recent Over-the-Counter Innovations’, Journal of Money, Credit and Banking, 31(3), Part 2: The Role of Central Banks in Money and Payments Systems, August 1999, 596-618.

⁵A. Khwaja, ‘Default at Nasdaq Clearing’, https://www.clarusft.com/default-at-nasdaq-clearing/(accessed 6 February 2019).

⁶ⁱBank for International Settlements Committee on Payments and Market Infrastructures (CPMI) and Board of the International Organization of Securities Commissions (IOSCO), Principles for financial market infrastructures, April 2012.

⁷Bank for International Settlements Committee on Payments and Market Infrastructures (CPMI) and Board of the International Organization of Securities Commissions (IOSCO), Resilience of central counterparties (CCPs): Further guidance on the PFMI, July 2017.

⁸D. Hughes and M. Manning, ‘CCPs and Banks: Different Risks, Different Regulations’, Reserve Bank of Australia, Bulletin, December Quarter 2015.

⁹E. Nosal and R. Steigerwald, ‘What is clearing and why is it important?’, Chicago Fed Letter, Number 278, September 2010.

¹⁰R. Cox and R. Steigerwald, ‘A CCP is a CCP is a CCP,’ Working Paper, Federal Reserve Bank of Chicago, April 2017.

¹¹D. Hughes and M. Manning, ‘CCPs and Banks: Different Risks, Different Regulations’, Reserve Bank of Australia, Bulletin, December Quarter 2015.

¹²R. Cox and R. Steigerwald, ‘A CCP is a CCP is a CCP,’ Working Paper, Federal Reserve Bank of Chicago, April 2017.

¹³Eurex Clearing, http://www.eurexclearing.com/clearing-en/risk-management/default-waterfall(accessed 24 January 2019).

¹⁴Bank for International Settlements Basel Committee on Banking Supervision (BCBS) and Board of the International Organization of Securities Commissions (IOSCO), Margin requirements for non-centrally cleared derivatives, March 2015.

¹⁵P. Haene and A. Sturm, ‘Optimal Central Counterparty Risk Management’, Swiss National Bank Working Paper 2009-07, June 2009.

¹⁶Bank for International Settlements Basel Committee on Banking Supervision (BCBS) and Board of the International Organization of Securities Commissions (IOSCO), Margin requirements for non-centrally cleared derivatives, March 2015.

¹⁷R. Cox and R. Steigerwald, ‘A CCP is a CCP is a CCP,’ Working Paper, Federal Reserve Bank of Chicago, April 2017.

¹⁸V. Vaghela, ‘Korea clearing structure in question after HanMag trading error’, Risk.net, 5 March 2014.

¹⁹J. Grant and P. Stafford, ‘Banks launch clearing review after Korean broker default’, Financial Times, 7 March 2014.

²⁰Korea Exchange (KRX), https://tglobal.krx.co.kr/contents/GLB/06/0608/0608050501/GLB0608050501.jsp(accessed 10 February 2019).

²¹US Commodities and Futures Trading Commission, CFTC Letter Number 17-51, 12 October 2017

https://www.cftc.gov/sites/default/files/idc/groups/public/@lrlettergeneral/documents/letter/17-51.pdf(accessed 11 February 2019)

²²Bank for International Settlements Committee on Payments and Market Infrastructures (CPMI) and Board of the International Organization of Securities Commissions (IOSCO), Principles for financial market infrastructures, April 2012.

²³Bank for International Settlements Committee on Payments and Market Infrastructures (CPMI) and Board of the International Organization of Securities Commissions (IOSCO), Principles for financial market infrastructures, April 2012.

²⁴Bank for International Settlements Committee on Payments and Market Infrastructures (CPMI) and Board of the International Organization of Securities Commissions (IOSCO), Resilience of central counterparties (CCPs): Further guidance on the PFMI, July 2017.

²⁵CME Group, CME SPAN®: Standard Portfolio Analysis of Risk®, https://www.cmegroup.com/clearing/files/span-methodology.pdf(accessed 27 January 2019).

²⁶R. Barker, A. Dickinson, A. Lipton, and R. Virmani, ‘Systemic risks in CCP networks’, Risk.net, 5 January 2017.

²⁷J. Hull and A. White, ‘Incorporating volatility updating into the historical simulation method for value and risk,’ Journal of Risk, Fall 1998.

²⁸L. Paulson and J. Starn, ‘Nordic Power Whale Losses Are Blow to World’s Oldest Market’, 14 September 2018, www.bloomberg.com(accessed 6 February 2019).

²⁹Nasdaq Clearing, https://business.nasdaq.com/updates-on-the-Nasdaq-Clearing-Member-Default/index.html(accessed 6 February 2019).

³⁰Office of the Superintendent of Financial Institutions (Canada), Enterprise-Wide Model Risk Management for Deposit-Taking Institutions, September 2017.

³¹L. Paulsson and M. Holter, ‘Phantom Trader Who Blew Hole in World’s Oldest Power Market’, 15 September 2018, www.bloomberg.com(accessed 11 February 2019).

³²R. Cox and R. Steigerwald, ‘A CCP is a CCP is a CCP,’ Working Paper, Federal Reserve Bank of Chicago, April 2017.

³³Bank for International Settlements Committee on Payments and Market Infrastructures (CPMI) and Board of the International Organization of Securities Commissions (IOSCO), Principles for financial market infrastructures, April 2012.

³⁴D. Duffie, ‘Resolution of Failing Central Counterparties’, Working Paper, Graduate School of Business, Stanford University, 17 December 2014.

³⁵See, for example, LCH Limited Default Rules, September 2017, https://www.lch.com/system/files/media_root/Default%20Rules.pdf(accessed 12 February 2019).

³⁶D. Duffie, ‘Resolution of Failing Central Counterparties’, Working Paper, Graduate School of Business, Stanford University, 17 December 2014.

³⁷Concern about what would happen if a CCP should fail is not purely theoretical. Three CCPs have failed since 1974, albeit none in the United States. The most recent of these failures occurred in 1987. See R. Cox and R. Steigerwald, ‘A CCP is a CCP is a CCP,’ Working Paper, Federal Reserve Bank of Chicago, April 2017.

About the Author: David Oakes

David Oakes is a specialist in the design and delivery of financial learning programs in equity, rates, credit, and commodity markets. He is also the president of a financial markets consultancy based in Montreal, Canada. David has presented a wide range of programs to financial institutions, securities exchanges, regulators and corporate clients worldwide with a special emphasis on derivative securities, fixed income and risk management.

David is the course author and principal trainer for the International Capital Markets Association (ICMA) Fixed Income Certificate (FIC) program, a leading qualification for finance professionals. From 1998 to 2004, he was Director of Academic and Professional Education at the ICMA Centre at the University of Reading in the United Kingdom, where he developed, managed and taught on the Centre’s postgraduate finance programs and professional education programs. Prior to 1998, he was a lecturer in finance at Warwick Business School, the University of Reading and the University of Exeter in the United Kingdom, specializing in asset pricing and derivatives modeling.

David has been involved in financial markets training and consulting since 1993. From 1998 to 2004, he was Director of Academic and Professional Education at the ICMA Centre at the University of Reading in the United Kingdom. He developed, managed and taught on the Centre’s postgraduate finance courses and was responsible for professional education, including the ICMA International Fixed Income and Derivatives (IFID) Certificate and Operations Certificate. Prior to 1998, he was lecturer in finance at Warwick Business School, the University of Reading and the University of Exeter, specializing in asset pricing and derivatives modeling.

David graduated from the University of Alberta (Canada) with a BA (Honours) in Economics. He also obtained an MSc (Econ) from the London School of Economics and Political Science (United Kingdom).

David is a former member of the Bond and Fixed Interest Markets examination panel of the Securities and Investment Institute (United Kingdom).

Copyright © 2019 by Global Financial Markets Institute, Inc.

PO Box 388

Jericho, NY 11753-0388

+1 516 935 0923

www.GFMI.com

 

Download article